1.     Introduction

The field of engineering design has undergone substantial evolution over the years. Due to this development, optimization techniques have also experienced significant growth. Genetic Algorithms (GAs), Evolutionary Algorithms (EAs), and strategies like the Pareto front have been developed with inspiration from the natural selection concept. One of the changes that occurred in recent decades was the number of objective functions to be optimized simultaneously. Single Objective Optimization (SOO), considered a conventional way of optimization, focuses on optimizing each metric individually. In contrast, Multi-Objective Optimization (MOO) focuses on optimizing more than one objective function together. The rise in the number of target points that architectural designers must cover, such as thermal regulation, energy efficiency, and economic sustainability, has increased the popularity of Multi-Objective Optimization as a robust algorithm. As a result, implementing Single Objective Function or Multi-Objective Optimization in architectural initiatives become a significant challenge. The decision of whether to use MOO’s powerful features with increased complexity or not has caused designers to consider their options. Therefore, it is essential to comprehend the benefits and drawbacks of both SOO and MOO to determine which method can satisfy the designer’s objectives. This article will concentrate on solutions which are combining methods to create a hybrid optimization algorithm and developing an AI-based tool to determine the preferability of MOO or SOO.

2.     Background of The Problem

         Designers find it challenging to manage trade-offs related to performance standards and constraints when creating a performance-based design.  Optimization methods provide different approaches to dealing with each performance parameter, such as Life-Cycle Cost, Solar Accessibility, and Thermal Comfort. Choosing the proper genetic algorithm is necessary to meet the performance-based expectations and find the optimal design shape while considering the common interest of parameters. The problem is judging which optimization method would be more beneficial for specific projects. MOO's primary advantage is that it enables designers to consider several objective functions simultaneously. It may identify solutions that compromise many objective functions, providing designers with various possibilities. MOO contains much complexity, requires much processing, and finding the best answer quickly is difficult compared to SOO. Designers might find it challenging to make well-informed conclusions regarding the best solution with MOO. On the other hand, SOO has the benefit of being more comprehensible and computationally compelling. However, it may need to convey the intricacy of actual design challenges fully. The criteria to evaluate any solution for this problem would be whether the solution supports the designer in choosing which would be more beneficial.

3.     Solution 1: A Hybrid Optimization Algorithm: MWDEO

        Combining multi-objective and single-objective optimization methods to create a hybrid optimization algorithm has been proposed as a solution to the problem explained. Hybrid Optimization Algorithm seeks to define a new efficient approach using the benefits of both optimization algorithms. MWDEO is one of the hybrid optimization algorithms which explores the search space in a better way. The indicated method, MWDEO, combines the Whale Optimization Algorithm, Opposition-Based Learning, and Differential Equation Algorithm to create a hybrid multi-objective optimization method (Ewees, Elaziz, and Oliva, 2020). Whale Optimization Algorithm, which was proposed as a solution to single-objective problems, imitates the humpback whales' hunting strategies. Opposition-Based Learning computes a solution's opposite value and then compares it to the original solution to determine which is the best in the search space (Ewees, Elaziz, and Oliva, 2020). Differential Equation Algorithm, on the other hand, is one of the most frequently employed optimization techniques that make quick use of elementary operators to find the best single objective answer. The findings of the experiments indicate that MWDEO is an appropriate approach for optimization problems. Figure 1 demonstrates how MWDEO outperforms other methods in terms of CPU time for addressing the WFG problem, which is a test suite to evaluate the functionalities of algorithms. The key feature of the MWDEO for designers is an improvement in convergence capabilities with Opposition-Based Learning and Differential Equation Algorithm to utilize the search space. Figure 2 demonstrates how the MWDEO algorithm shows superior performance against other algorithms over WFG5 test problem which is another test suite with a concave optimal geometry.

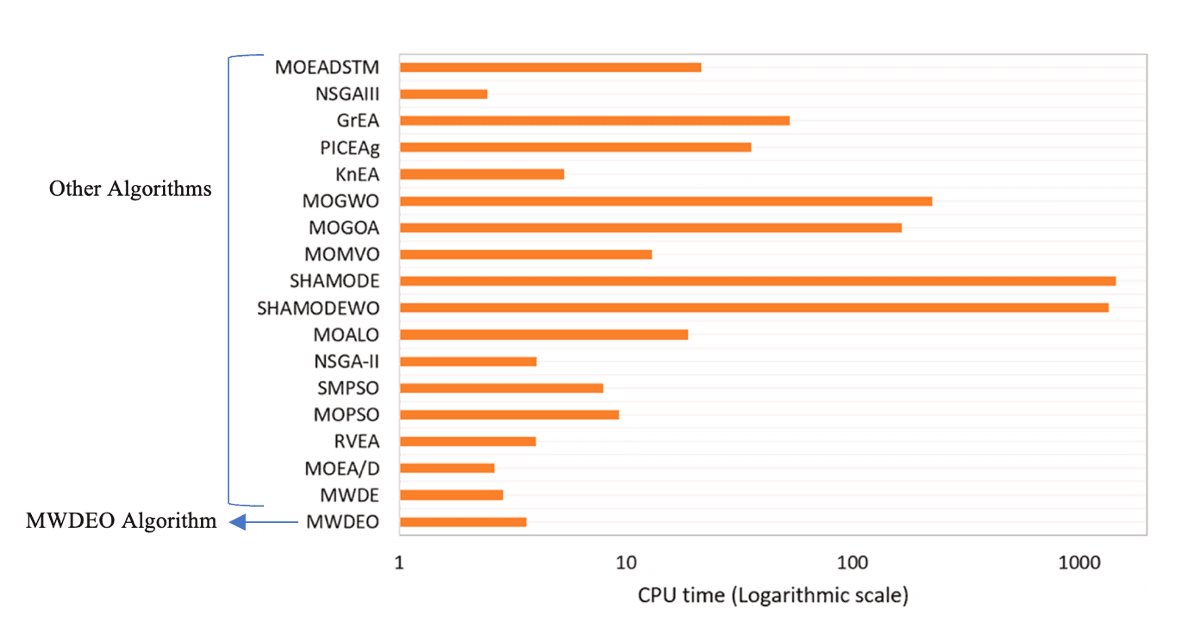
Figure 1. The consuming CPU time by each algorithm in solving the WFG problem. (Ewees, Elaziz, and Oliva, 2020). 

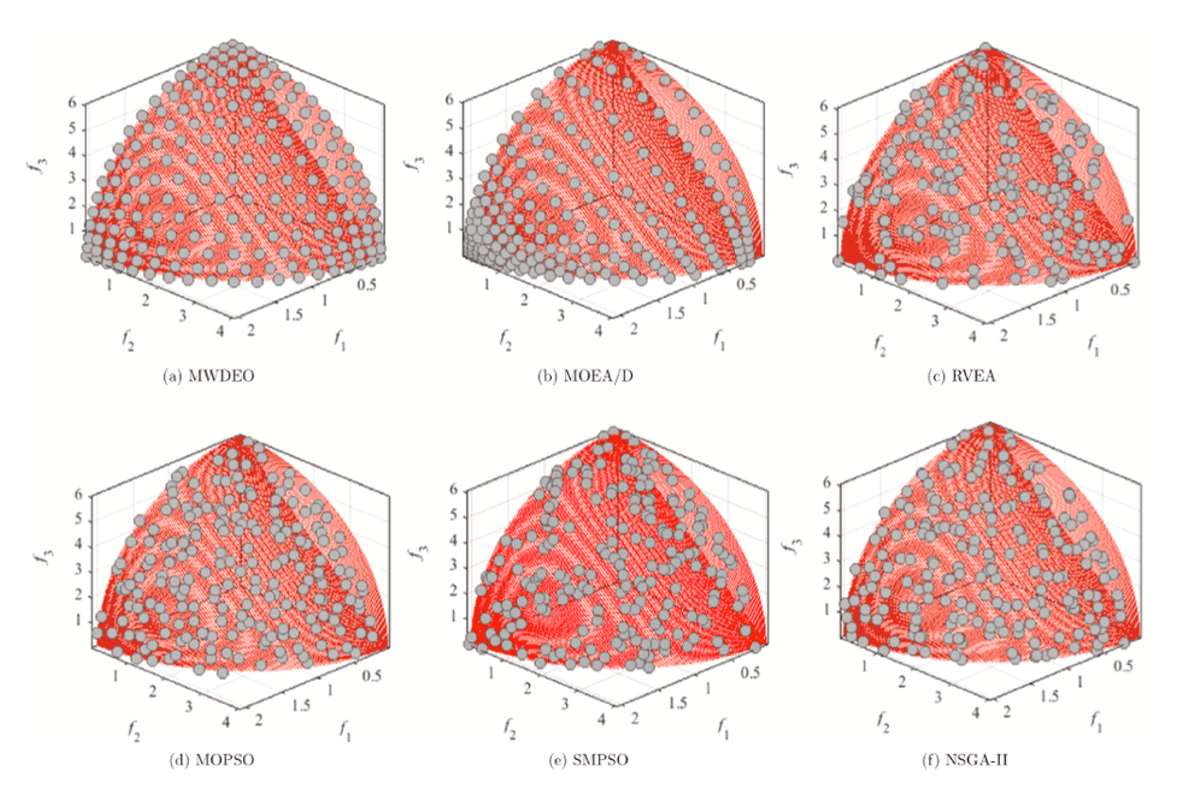
Figure 2. The results of WFG5 test suite over algorithms. (Ewees, Elaziz, and Oliva, 2020).

4.     Solution 2: AI-Based Tool for Prediction

An AI-based tool can be developed to determine the preferability of MOO or SOO for a particular architectural design procedure. The algorithm can be trained on a collection of design problems that have been optimized using either MOO or SOO, considering the properties of the design task, such as the quantity and complexity of the goal functions. The dataset would need to include features such as the building type, location, size, number of floors, construction materials, and energy performance targets and the corresponding optimization outcome. The program can be developed using Supervised Learning and Deep Reinforcement Learning to train a machine learning model on a sizable dataset of annotated design challenges (Li, Zhang, and Wang, 2020). The model can take input features such as the quantity and intricacy of the goal functions and available optimization resources to produce a binary categorization. As seen in Figure 3, an AI-based algorithm can use inserted formulas to evaluate the performance of each optimization method mathematically. Overall Performance Indicator can be mathematically calculated for each optimization algorithm and represented to the designer as a table that shows each algorithm's positive/negative sides (Si, Wang, Yao, Shi, Jin, Zhou, 2019). Designers can formulate different equations to calculate the distinct performance of each parameter. Once trained, the model can forecast the best optimization strategy for new design problems. By inputting the characteristics of the task, the model can determine whether MOO or SOO is more appropriate, saving designers time and effort in choosing the best optimization strategy for a particular design problem. In addition, this AI-based technique can provide superior refining outcomes by selecting the most suitable approach.

Figure 3 Overall Performance Indicator Calculation Sample Formula Si, Wang, Yao, Shi, Jin, Zhou, 2019).

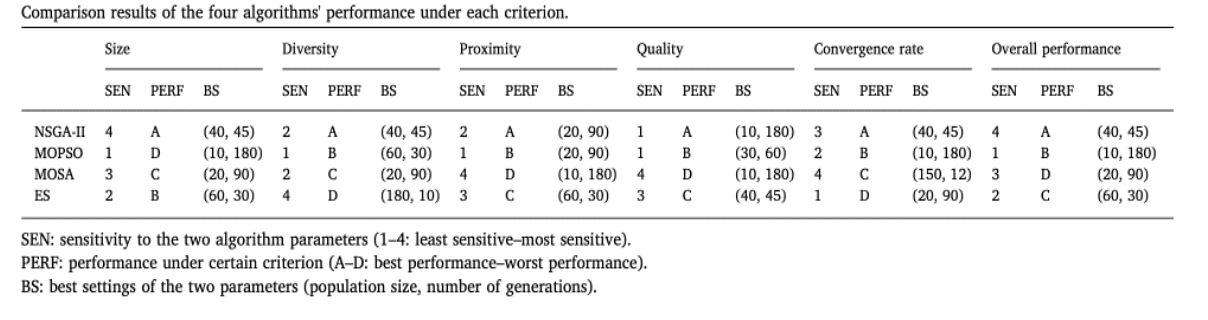
Figure 4 Example Output of AI-Based Performance Indicator (Si, Wang, Yao, Shi, Jin, Zhou, 2019).

5.     Evaluation of Solutions

         Developing an AI tool to determine the optimization approach for a particular design is a solution that is applicable and effective. However, the hybrid optimization method may become a more practical option for designers, especially when an AI tool can only identify the appropriate optimization method (SOO or MOO). As indicated in Section 4, the AI model can forecast the proper optimization method by inputting the features of the task. In contrast, the hybrid optimization method has the potential to perform better than using SOO or MOO alone. With proper exploitation of the most significant regions and effective operators, MWDEO has the benefits of performing extensive exploration of the search space (Ewees, Elaziz, and Oliva, 2020). MWDEO shows superior performance against unaccompanied SOO and MOO in experiments. As shown in Section 3, the hybrid optimization method, MWDEO, outperforms other optimization methods in overall performance. Other hybrid optimization methods that combine efficient sides of SOO and MOO might also increase the performance and create an optimal design. Therefore, looking into this approach more thoroughly and seeing how it can result in the best possible design of buildings might be worthwhile.

6.     Conclusion

         The excessive development of architectural features makes it difficult for designers to determine which optimization method to utilize. This can make the optimization process less efficient and increase the difficulty of designers to choose an optimal method for a given design. This study offers two solutions to this problem: a hybrid optimization approach for SOO-MOO and an AI tool that can guide architecture designers on the best optimization method. Ultimately, both approaches can improve optimization and help designers in selecting the most beneficial approach. The hybrid optimization method, however, can be a better choice for designers who must maintain a specific structure.

References:

Altay, Elif Varol. Alataş, Bilal. (2019) “Performance Analysis of Multi-Objective Artificial Intelligence Optimization Algorithms In Numerical Association Rule Mining”. Journal of Ambient Intelligence and Humanized Computing, 2020, 11:3449–3469, https://doi.org/10.1007/s12652-019-01540-7.

Ewees, Ahmed A.. Elaziz, Mohamed Abd. Oliva, Diego. (2020) “A new multi-objective optimization algorithm combined with opposition-based learning”. Expert Systems with Applications, vol. 165, 2021, https://doi.org/10.1016/j.eswa.2020.113844.

Li, Kaiwen. Zhang, Tao. and Wang, Rui. (2020) Deep Reinforcement Learning for Multi-Objective Optimization. Journal Of IEEE Transcations On Cybernetics 2020, DOI:                  10.1109/TCYB.2020.2977661.

Si, Binghui. Wang, Jianguo. Yao, Xinyue. Shi, Xing, Jin, Xing. Zhou, Xin. (2019) “Multi-Objective Optimization Design of a Complex Building Based On An Artificial Neural Network and Performance Evaluation of Algorithms”. Advanced Engineering Informatics, vol. 40, April 2019, p. 93-109, https://doi.org/10.1016/j.aei.2019.03.006.